卡尔丹诺在数学史上的作用:卡尔丹公式是指 方程求根公式
因为而,所以它们的和就正好为4这一事例有力地证明了虚数并不是完全没有用途的,至少我们在解方程的过程中可以通过它而得到正确的根这时,卡尔丹诺认为虚数在数学实践中确实有某种用途,但还是认为虚数是不可思议的
因为而,所以它们的和就正好为4这一事例有力地证明了虚数并不是完全没有用途的,至少我们在解方程的过程中可以通过它而得到正确的根这时,卡尔丹诺认为虚数在数学实践中确实有某种用途,但还是认为虚数是不可思议的,因此他称之为诡辩数对于虚数的这种奇妙作用,大数学家莱布尼兹也不得不感叹道。
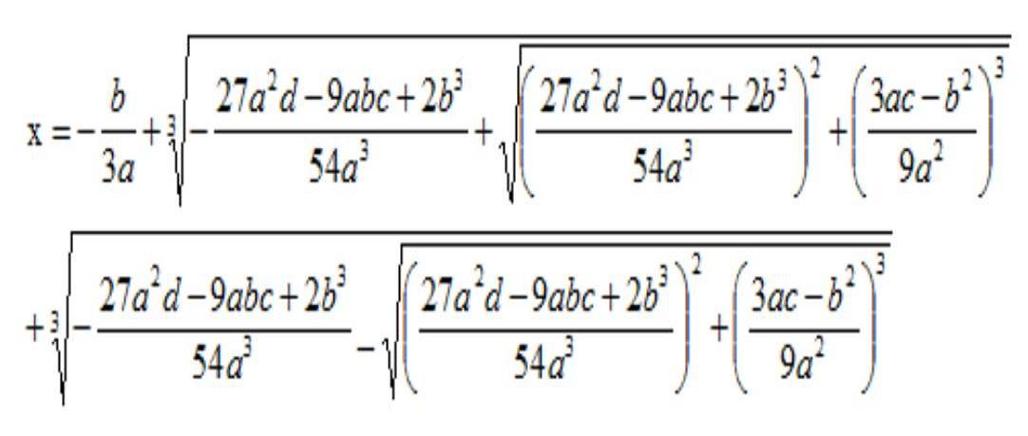
(图片来源网络,侵删)
怎样列出代数方程来解文字题,虽是十分古老的题材,但是它在数学发展史上曾起过重大作用,促进了代数学的发展和牛顿的观点一样,欧拉并不认为解决这类初等数学问题是有损尊严的事,在他的名著代数基础中就着意搜集了许多题目下面就是他的一个题目“一位父亲临死时叫他的几个孩子按照下列方式瓜分他的财产第。
316世纪,意大利数学家卡尔丹诺发明了三次方程的解法,并创造了“代数”这个术语来描述这种新的数学分支随着时间的推移,方程的概念逐渐发展并被广泛应用于各个领域如今,方程已经成为现代数学中的一个重要分支,不仅在解决实际问题中发挥着重要作用。
他的做法是划时代的,从而奠定了代数学的基础,对代数的国际通用语言的形成起到了极为重要的作用1591年,韦达出版了他的代数学专著分析方法入门,这是历史上第一部符号代数学它明确了“类的算术”和“数的算术”的区别,即代数与算术的分界线据载,韦达还以他精湛的数学知识,为国家赢得了。
他对天文学数学有着浓厚的兴趣,经常利用业余时间研究数学1584年到1589年,由于他在政治上处于反对派地位,被免去了官职从此,他便专心致力于数学的研究在从政期间,韦达研究丢番图塔尔塔利亚卡尔丹诺邦别利斯提文等人的著作他从这些名家,特别是从丢番图那里,获得了使用字母的想法在。
卡尔丹未征得冯塔纳的同意私自发表,并且将其名字略去,剽窃他人的学术成果,据为已有,确实是数学史上不光彩的一幕不过,历。